Number patterns

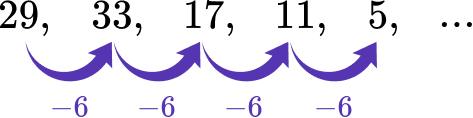
Here you will learn about number patterns, including how to find and extend rules for sequences, input/output tables and shape patterns.

Students will first learn about number patterns as part of operations and algebraic thinking in 4th and 5th grade. They continue to build on this knowledge in middle school and high school.

What are number patterns?

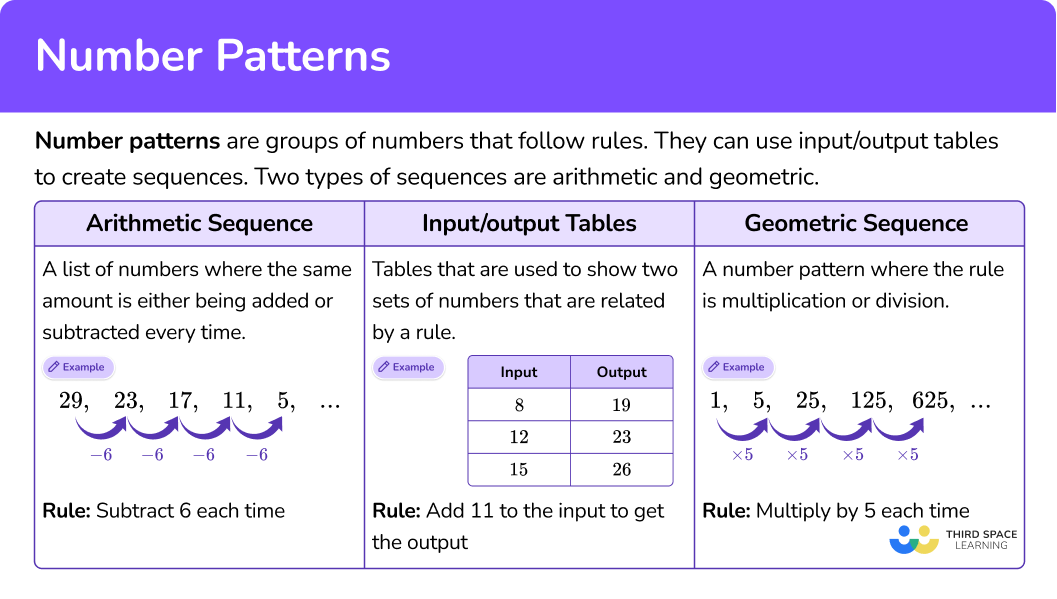
Number patterns are groups of numbers that follow rules. They can use input/output tables to create sequences.

Two types of sequences are arithmetic and geometric.

• An arithmetic sequence is a list of numbers where the same amount is either being added or subtracted every time.

Each sequence has a starting number, a rule and terms (the numbers that make up the sequence).

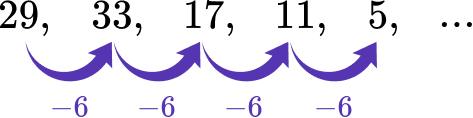
Rule: Subtract 6 each time.

There are also patterns, between the terms of two or more arithmetic sequences.

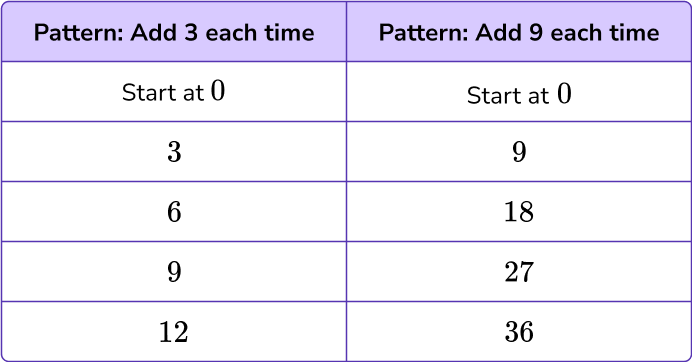
Both sequences start at 0. If you multiply the left column by 3, you get the terms in the right column.

This is because using the rule +9 is three times more than the rule +3.

Step-by-step guide: Arithmetic sequence

• A geometric sequence is a number pattern where the rule is multiplication or division.

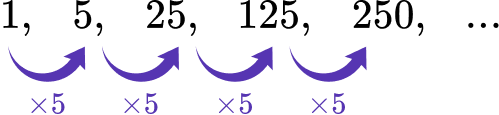
Rule: Multiply the previous term by 5.

Rule: Divide the previous term by 3.

Step-by-step guide: Sequences

This page will highlight rules that involve whole numbers only.

[FREE] Number Patterns Worksheet (Grade 4 to 5)

Use this quiz to assess your grade 4 to 5 students’ understanding of number patterns. 10+ questions with answers on 4th and 5th grade number pattern topics to identify areas of strength and support!

[FREE] Number Patterns Worksheet (Grade 4 to 5)

Use this quiz to assess your grade 4 to 5 students’ understanding of number patterns. 10+ questions with answers on 4th and 5th grade number pattern topics to identify areas of strength and support!

• Input/output tables are tables that are used to show two sets of numbers that are related by a rule. The rule can be one step or multi-step, but has to work for each relationship shown in the table.

What is the rule for the table below?

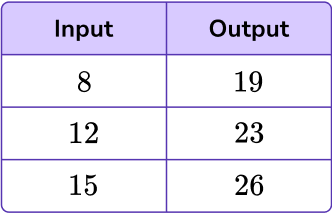
To find the rule, look for the relationship between the input and the corresponding output.

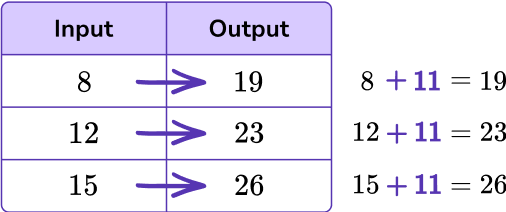
Notice, 11 is being added to each input to get the output, so the rule is ‘add 11. ’

Step-by-step guide: Input/output tables

As students learn to work with number patterns, they can learn more about generalizing patterns by working with shape patterns.

• Shape patterns are any set of polygons, 3D shapes, letters or symbols that follow non-operational rules. There are repeating shape patterns and growing shape patterns.

A repeating pattern has a core that repeats over and over again.

The core of the pattern above is:

The core can be used to extend the pattern.

The next shape in the pattern would be:

because the last part of the core shown is:

.

• A growing pattern has parts that stay the same, but other parts that change.

• Changing – the left column starts with 0 and increases by 2.
• Staying the same – the 1 cube on the top right.

Step-by-step guide: Shape patterns

What are number patterns?

Common Core State Standards

How does this relate to 4th grade math and 5th grade math?

Grade 4 – Operations and Algebraic Thinking (4.OA.C.5)
Generate a number or shape pattern that follows a given rule. Identify apparent features of the pattern that were not explicit in the rule itself.

Grade 5 – Operations and Algebraic Thinking (5.OA.B.3)
Generate two numerical patterns using two given rules. Identify apparent relationships between corresponding terms. Form ordered pairs consisting of corresponding terms from the two patterns, and graph the ordered pairs on a coordinate plane.

How to use number patterns

There are a lot of ways to use number patterns. For more specific step-by-step guides, check out the pages linked in the “What are number patterns?” section above or read through the examples below.

Number patterns examples

Example 1: geometric sequence

What are the next three terms in the pattern?

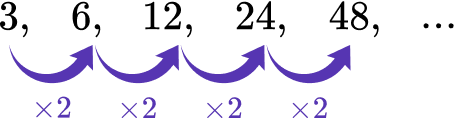
Rule: Multiply the previous term by 2.

2 Use the rule to extend the pattern.

Multiply the last term by 2 to extend the pattern to the next three terms.

3 State and explain any patterns within the terms.

Except for the first term, all the terms are even.

The first term is odd, but multiplying it by 2 (even), makes the next term even.

From then on it is always an even term times 2 \rightarrow \text < even >\times \text < even >=\text < even >.

Example 2: compare arithmetic sequences

Compare the following sequences:

0, 2, 4, 6, 8… \, and \, 0, 12, 24, 36, 48…

Identify the rule of each sequence.

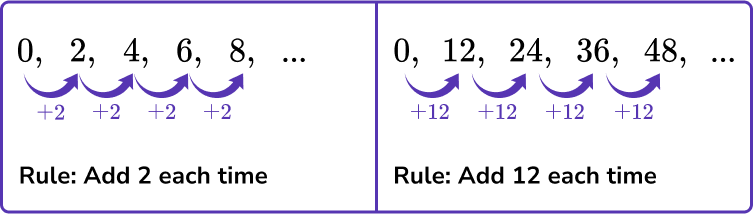
Find a pattern between the related terms of each sequence.

Look at the related terms for each sequence. What do you notice?

Both sequences start at 0. If you multiply the left column by 6, you get the terms in the right column.

Use the pattern to write a comparison statement.

The terms in the second sequence are 6 times the terms in the first sequence.

This is because using the rule +12 is six times more than using the rule +2.

Example 3: input/output table – identify the rule

What is the rule for the table?

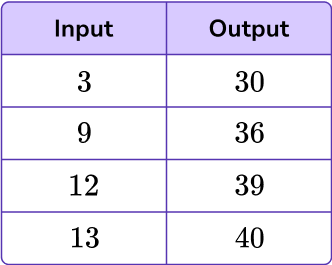
Look at the relationship between the input and the corresponding output.

Looking from each input to output, see if you notice an obvious relationship. If not, use subtraction to find the difference between each input and the corresponding output.

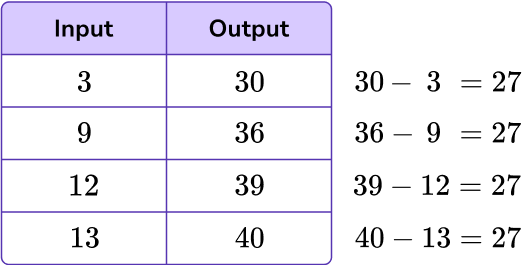
Decide if the rule is add/subtract or multiply/divide.

Each output is 27 more than the input, so the rule is addition.

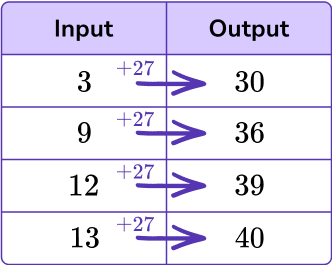
Write the rule.

Rule: Add 27 to the input.

Example 4: input/output table – find a missing value

Find the missing value in the table.

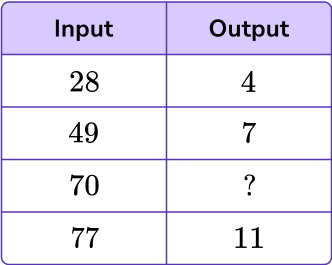
Look at the relationship between the input and the corresponding output.

Looking from each input to output, see if you notice an obvious relationship. If not, use subtraction to find the difference between each input and the corresponding output.

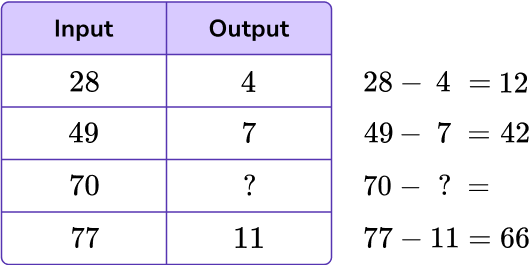
Decide if the rule is add/subtract or multiply/divide.

From each input to output, the difference is not the same, so the rule is not addition or subtraction.

Try to find a relationship that involves multiplying or dividing. Since the relationship from input to output is decreasing, try division.

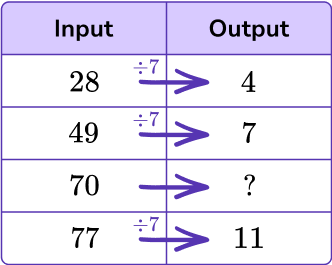
Write the rule.

Rule: Divide the input by 7.

*Note, the rule ‘Multiply the input by \, \cfrac \, ’ is also correct.

Use the rule to find the missing value(s).

The missing value in the table is 10.

Example 5: 3D shape pattern, repeating

Create a rule for the pattern and find the next shape.

Identify the core – the part of the pattern that repeats.

This is a repeating pattern with cubes that go purple, purple, orange, purple, red, purple.

Notice that purple is repeated multiple times within the core. Always look at all the shapes given to confirm the pattern core.

Use the core to find and justify the next part in the pattern.

The next shape is:

because the last part of the core shown is:

Example 6: shape pattern, growing

Create a rule for the pattern and find the next shape.

Identify what is changing and what is staying the same.

• Changing – 0 triangles on the top and left side, 1 triangle on top and left side, 2 triangles on top and left side, 3 triangles on top and left side.
• Staying the same – The first triangle at the bottom is always there.

Create a rule based on Step 1.

Start with 1 triangle. Add 1 triangle to the top and 1 triangle to the left side each time.

Use the rule to find and justify the next part in the pattern.

The next part in the pattern is:

because 1 triangle is added to the top and 1 triangle is added to the side each time.

Teaching tips for number patterns

• There are many printable number patterns worksheets that can be used, but also give students the opportunity to create their own patterns. Then let their classmates find the rules and extend them.

• Support students who are not yet confident in all operations by providing useful tools such as number lines, hundreds boards or counters. Completing calculations should not be a burden when working with patterns.

Focusing on justifying pattern rules is as important as identifying them. Justification is not only a necessary mathematical practice, but doing it can teach students how to write better rules.

Easy mistakes to make

• Writing a rule for a sequence that is not term to term
  Work with sequences in elementary school is recursive. Therefore, it is important to focus on what is happening from term to term in order to define the rule. This can be confusing when an arithmetic sequence is a list of multiples.

For example,
What is the rule for the pattern 10, 20, 30, 40, 50?

To find the next term, you need to add 10, not multiply.
Even though the terms are multiples of 10, for this to be the rule, there would need to be corresponding inputs and outputs, such as…

Using only the first number and second number to create the rule
Often by the third number the pattern can be identified, but it is still important to look at all of the numbers in a pattern before finalizing the rule. Looking at just too few can lead to the incorrect rule.

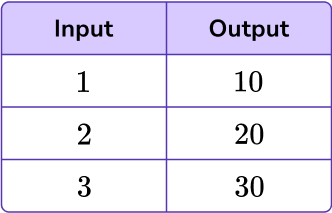
For example,
What is the rule for the pattern 3, 6, 12, 24, 28?

• Making an operational error
  Since finding the rule and extending the pattern require a calculation, this leaves room for mistakes to be made. Always double check your work and take time to think about if your answers are reasonable.

• Thinking there is only one way to write a growing shape pattern rule
  Often there is more than one way to describe what is changing and what is staying the same in a growing shape pattern. Encourage students to look for more than one way to describe their rule, as this is a helpful stepping stone to equivalent expressions.